How to Continually Look for a Broadcast but Not Block Python

The term broadcasting refers to how numpy treats arrays with different Dimension during arithmetic operations which lead to certain constraints, the smaller array is broadcast across the larger array so that they have compatible shapes.
Broadcasting provides a means of vectorizing array operations so that looping occurs in C instead of Python as we know that Numpy implemented in C. It does this without making needless copies of data and which leads to efficient algorithm implementations. There are cases where broadcasting is a bad idea because it leads to inefficient use of memory that slow down the computation.
Example –

Python3

import numpy as np

a = np.array([ 5 , 7 , 3 , 1 ])

b = np.array([ 90 , 50 , 0 , 30 ])

c = a * b

print (c)

Example to get deeper understanding –
Let's assume that we have a large data set, each datum is a list of parameters. In Numpy we have a 2-D array, where each row is a datum and the number of rows is the size of the data set. Suppose we want to apply some sort of scaling to all these data every parameter gets its own scaling factor or say Every parameter is multiplied by some factor.
Just to have some clear understanding, let's count calories in foods using a macro-nutrient breakdown. Roughly put, the caloric parts of food are made of fats (9 calories per gram), protein (4 cpg) and carbs (4 cpg). So if we list some foods (our data), and for each food list its macro-nutrient breakdown (parameters), we can then multiply each nutrient by its caloric value (apply scaling) to compute the caloric breakdown of every food item.

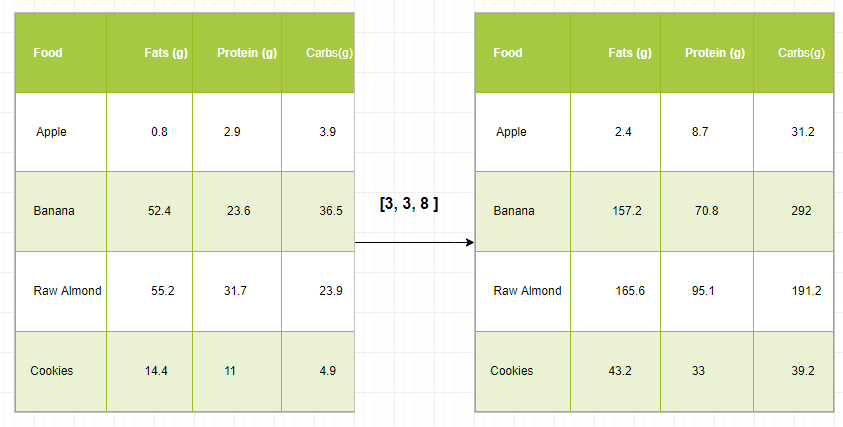
With this transformation, we can now compute all kinds of useful information. For example, what is the total number of calories present in some food or, given a breakdown of my dinner know how much calories did I get from protein and so on.
Let's see a naive way of producing this computation with Numpy:

Python3

macros = array([

[ 0.8 , 2.9 , 3.9 ],

[ 52.4 , 23.6 , 36.5 ],

[ 55.2 , 31.7 , 23.9 ],

[ 14.4 , 11 , 4.9 ]

])

result = zeros_like(macros)

cal_per_macro = array([ 3 , 3 , 8 ])

for i in range (macros.shape[ 0 ]):

result[i, :] = macros[i, :] * cal_per_macro

result

output:

array([[   2.4,    8.7,   31.2 ],        [  157.2,   70.8,  292 ],        [   165.6,  95.1,   191.2],        [   43.2,   33,    39.2]])

Algorithm:

Inputs: Array A with m dimensions and array B with n dimensions

p = max(m, n) if m < p:     left-pad A's shape with 1s until it also has p dimensions  else if n < p:     left-pad B's shape with 1s until it also has p dimensions result_dims = new list with p elements  for i in p-1 ... 0:     A_dim_i = A.shape[i]     B_dim_i = B.shape[i]     if A_dim_i != 1 and B_dim_i != 1 and A_dim_i != B_dim_i:         raise ValueError("could not broadcast")     else:         # Pick the Array which is having maximum Dimension         result_dims[i] = max(A_dim_i, B_dim_i)        

Broadcasting Rules:
Broadcasting two arrays together follow these rules:

1. If the arrays don't have the same rank then prepend the shape of the lower rank array with 1s until both shapes have the same length.
2. The two arrays are compatible in a dimension if they have the same size in the dimension or if one of the arrays has size 1 in that dimension.
3. The arrays can be broadcast together iff they are compatible with all dimensions.
4. After broadcasting, each array behaves as if it had shape equal to the element-wise maximum of shapes of the two input arrays.
5. In any dimension where one array had size 1 and the other array had size greater than 1, the first array behaves as if it were copied along that dimension.

Example #1: Single Dimension array

Python3

import numpy as np

a = np.array([ 17 , 11 , 19 ])

print (a)

b = 3

print (b)

c = a + b

print (c)

Output:

[17 11 19] 3 [20 14 22]

Example 2: Two Dimensional Array

Python3

import numpy as np

A = np.array([[ 11 , 22 , 33 ], [ 10 , 20 , 30 ]])

print (A)

b = 4

print (b)

C = A + b

print (C)

Output:

[[11 22 33]  [10 20 30]]  4 [[15 26 37]  [14 24 34]]

Example 3:

Python3

import numpy as np

v = np.array([ 12 , 24 , 36 ])

w = np.array([ 45 , 55 ])

print (np.reshape(v, ( 3 , 1 )) * w)

x = np.array([[ 12 , 22 , 33 ], [ 45 , 55 , 66 ]])

print (x + v)

print ((x.T + w).T)

print (x + np.reshape(w, ( 2 , 1 )))

print (x * 2 )

Output:

[[ 4  5]  [ 8 10]  [12 15]]  [[2 4 6]  [5 7 9]]  [[ 5  6  7]  [ 9 10 11]]  [[ 5  6  7]  [ 9 10 11]]  [[ 2  4  6]  [ 8 10 12]]

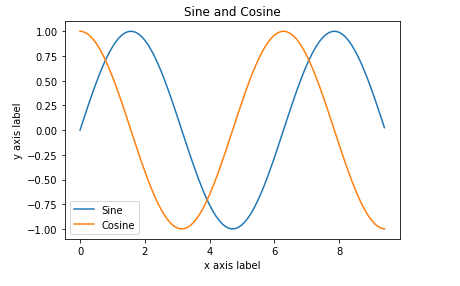
Plotting a two-dimensional function –
Broadcasting is also frequently used in displaying images based on two-dimensional functions. If we want to define a function z=f(x, y).
Example:

Python3

import numpy as np

import matplotlib.pyplot as plt

x = np.arange( 0 , 3 * np.pi, 0.1 )

y_sin = np.sin(x)

y_cos = np.cos(x)

plt.plot(x, y_sin)

plt.plot(x, y_cos)

plt.xlabel( 'x axis label' )

plt.ylabel( 'y axis label' )

plt.title( 'Sine and Cosine' )

plt.legend([ 'Sine' , 'Cosine' ])

plt.show()

Output:

amakerunfortalty1991.blogspot.com

Source: https://www.geeksforgeeks.org/python-broadcasting-with-numpy-arrays/

Share this post